Résoudre équation en ligne | Solveur d'équation

Résoudre équation en ligne


Entrez l'expression mathématique ...
log
clc
del
Calculer
ln
√
^
e
|---|
π
>
<
≥
≤
@
(
)
/
*
t
7
8
9
-
u
4
5
6
+
x
1
2
3
.
y
0
=
,
;

Le solveur d’équation est une excellente calculatrice capable de résoudre une grande variété de problèmes mathématiques.

Le solveur d’équation en ligne a été conçu pour être un outil d’aide à l’étude de l’algèbre. C’est donc la meilleure calculatrice pour résoudre des expressions algébriques de toutes sortes : équations du premier degré, équations du second degré, équations du troisième degré, équations logarithmiques, inéquations, systèmes d’équations, équations aux valeurs absolues, équations irrationnelles, etc.

Avec le solveur d’équation en ligne, vous pouvez simplifier et factoriser des polynômes, représenter graphiquement des fonctions et vérifier des solutions.

Pour apprendre à utiliser cette calculatrice et découvrir toutes ses fonctions, vous pouvez vous rendre sur le tutoriel que vous trouverez ci-dessous.

Resoudre equation en ligne : mode d'emploi

Cet outil de résolution d’équations en ligne possède une interface simple et intuitive, ce qui en fait un outil très facile à utiliser.

Résolvez des expressions algébriques de toutes sortes en deux étapes simples :

résoudre équation en ligne - mode d'emploi

Étape 1

Entrez des expressions algébriques dans le solveur d'équations, en utilisant le clavier de votre appareil ou en utilisant le clavier virtuel de la calculatrice elle-même. Vous remarquerez qu'au fur et à mesure que vous tapez l'expression algébrique, cette expression sera présentée dans un format plus naturel et lisible.

Étape 2

Une fois que vous avez fini de saisir l'expression ou l'équation algébrique correspondante, appuyez sur le bouton vert "Calculer" pour obtenir la solution étape par étape. Sous la solution se trouve le bouton rouge "Supprimer", qui vous aidera à tout supprimer afin que vous puissiez être prêt à résoudre un autre problème plus tard.

Ce qui précède peut être utilisé pour effectuer les tâches suivantes :

  • Résoudre des équations linéaires
  • Résoudre des équations quadratiques
  • Résoudre les inégalités
  • Fonctions graphiques
  • Décomposition de polynômes
  • Évaluer les équations
  • Opérations avec des polynômes
  • Résoudre des systèmes d’équations
  • Opérations avec des nombres complexes
  • Résoudre des équations avec des fractions
  • Résoudre des équations de valeur absolue
  • Opérations avec des fractions
  • Etc.

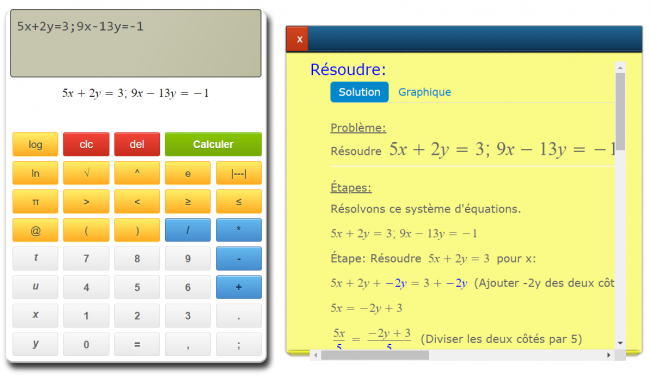
Résoudre des systèmes d'équations avec la calculatrice

Pour résoudre un système d’équations, insérez simplement les équations séparées par un point-virgule. Voici un exemple de résolution d’un système d’équations :

Systèmes d'equations

Qu'est-ce qu'une équation?

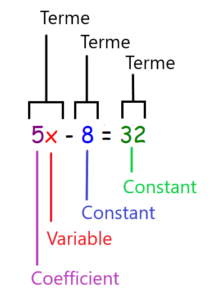
Mathématiquement, une équation peut être définie comme une déclaration qui représente l’égalité de deux expressions mathématiques, qui sont reliées par le signe égal « = ». Par exemple, 5x – 8 = 32  

Ici,

5x-8 et 32 sont des expressions

Le signe « = » relie les deux expressions.

Parties d'une équation

Pour présenter les parties d’une équation, nous utiliserons l’expression de l’exemple précédent :

Comment résoudre une équation

Résoudre des équations consiste à calculer la valeur de la variable inconnue qui satisfait l’égalité exprimée par l’équation. Pour savoir comment résoudre une équation, nous devons d’abord déterminer le type d’équation devant nous. Les principaux types d’équations sont : équations du premier degré, équations du second degré, équations rationnelles ou équations radicales.

Ensuite, nous expliquerons étape par étape comment résoudre les équations du premier et du second degré d’une variable.

Comment résoudre une équation du premier degré

Pour résoudre une équation du premier degré de la forme ax + b = c, où a, b et c sont des nombres réels, nous devons suivre ces étapes :
  1. Supprimez les parenthèses et utilisez la propriété distributive si nécessaire.
  2. Simplifiez les deux côtés de l’équation en combinant des termes similaires.
  3. S’il y a des fractions, multipliez les deux côtés de l’équation par le plus petit dénominateur commun de toutes les fractions.
  4. Déplacez les termes variables d’un côté de l’équation et les termes constants de l’autre côté en utilisant les propriétés d’addition et de soustraction de l’égalité.
  5. Si le terme contenant la variable a un coefficient autre que 1, divisez l’équation entière par la valeur de ce coefficient.
  6. Isolez la variable et obtenez la solution.
Nous allons maintenant montrer comment appliquer ce qui a été expliqué précédemment au moyen de l’exemple suivant :

Exemple : Résoudre l’équation
3(x + 4) = 24 + x

  • Nous simplifions l’équation en utilisant la propriété distributive.
    3x + 12 = 24 + x
  • Regroupez les termes similaires en utilisant la méthode de transposition.
    3x – x = 24-12
  • Simplifier à nouveau ⇒ 2x = 12
  • Maintenant, nous divisons tous les termes de l’équation par deux ⇒ 2x/2 = 12/2
  • Après avoir effectué toutes les étapes précédentes, nous avons la solution de l’équation, x = 6

Comment résoudre une équation du second degré

Lors de la résolution d’une équation du second degré de la forme ax2 + bx + c = 0, deux racines sont obtenues : α et β.

Pour résoudre ce type d’équations, nous pouvons appliquer trois méthodes différentes selon les cas :

  • Réécrire l’équation comme expression d’une identité remarquable
  • La méthode de factorisation
  • La méthode de la formule
 

Réécrire l’équation comme expression d’une identité remarquable

Parfois, nous pouvons manipuler l’équation pour la réécrire comme l’expression d’une identité remarquable, ce qui rend la résolution de l’équation beaucoup plus simple.

Une façon simple d’appliquer cette méthode est d’utiliser la formule suivante pour réécrire l’équation :

ax2 + bx + c ⇒ a(x + m)2 + n

où m est un nombre réel quelconque et n est un terme constant.

Pour implémenter cette formule dans l’expression ax2 + bx + c, on calcule d’abord la valeur de m et n :

m = b/2a  et  n = c – (b2/4a)

Remplacez ensuite ces valeurs par :

ax2 + bx + c = a(x + m)2 + n = 0

a(x + m)2 + n = 0

a(x + m)2 = – n

(x + m)2 = – n/a

(x + m) = ±√(- n/a)

x = ±√(- n/a) -m

 

Méthode de factorisation

Pour résoudre une équation du second degré à l’aide de la méthode de factorisation, procédez comme suit :

  • Écrivez l’équation donnée sous une forme standard et en divisant les termes moyens, factorisez l’équation.
  • Réécrire l’équation obtenue comme le produit de deux facteurs linéaires.
  • Fixez chaque facteur linéaire égal à zéro et résolvez pour x.

 

Méthode de la formule

Cette méthode consiste à extraire les coefficients de l’équation quadratique ax2+bx+c=0 et à les substituer dans la formule suivante :

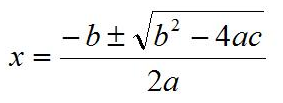
Formule résoudre une équation du second degré

♥ Fait avec amour ♥